Este artigo apresenta o uso do X-Machine RTO como ferramenta computacional a qual utiliza técnicas de Inteligência Artificial e Modelagem Matemática de Processos para resolver problemas na Geração de Energia em Usinas Termoelétricas, problemas principalmente de Despacho Econômico e Despacho Ambiental. Esses problemas têm que alocar a demanda de energia em unidades geradoras disponíveis sob as mesmas restrições operacionais. Algoritmos Genéticos (AG) foram eleitos como a metodologia para resolver esses problemas. Algumas modificações foram introduzidas nos Algoritmos Genéticos Clássicos (AGC) para adaptá-lo aos problemas de geração térmica. A codificação real foi usada para permitir a hibridização usando regras determinísticas. Um Algoritmo Genético Híbrido (AGH) foi criado através do operador de mutação que foi formulado usando a direção do gradiente modificado. Um algoritmo de controle de parâmetros foi adicionado ao AGH para evitar o ajuste inicial dos parâmetros. O algoritmo final desenvolvido foi denominado Algoritmo Genético Híbrido Auto Adaptativo. É capaz de resolver problemas não lineares com objetivo único, como Despacho Econômico e Despacho Ambiental; problemas com restrições lineares, como os limites operacionais e equilíbrios de força; e, finalmente, o problema com restrições não lineares, como o Despacho Econômico com Restrições Ambientais.
Todos os tipos de problemas considerados foram reunidos na solução X-Machine RTO para fornecer múltiplas opções aos planejadores e operadores do sistema de geração de energia.
1. INTRODUÇÃO
Na geração termelétrica existem três características importantes que devem ser combinadas, sendo:
i) Características Técnicas; ii) Características Econômicas; iii) Características Ambientais.
Essas características, entretanto, estão relacionadas às curvas de entrada-saída de cada unidade geradora.
1.1. Características Técnicas
A eficiência global das unidades térmicas é encontrada medindo a entrada de combustível e a saída de potência, em termos de uma taxa, gerando as curvas de entrada-saída. A Figura 1 mostra, aproximadamente, uma unidade de geração termelétrica. A entrada para a unidade apresentada, pode ser expressa em termos da quantidade de combustível convertida em calor por hora. A saída é, frequentemente, a saída da unidade de potência líquida, P(W). A Figura 1 apresenta uma taxa convexa e suave.
Curvas semelhantes são desenvolvidas para cada unidade geradora. Os dados necessários para encontrar a curva de entrada-saída podem ser obtidos no cálculo do projeto ou nos testes de taxa de calor. Quando os testes de taxa de calor são usados, os pontos encontrados não representam uma curva suave como mostrado na Figura 1.
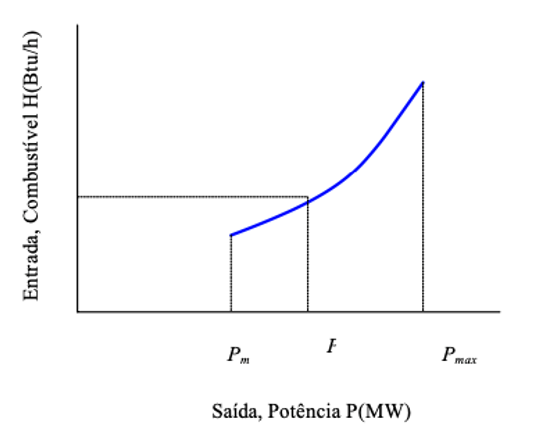
Figura 1: Curva de entrada-saída típica de uma unidade térmica
1.2. Características Econômicas
A curva da Figura 1 pode ser convertida em custo de combustível multiplicando a entrada de combustível pelo custo de combustível equivalente. O custo do combustível em uma unidade de geração térmica é considerado um custo variável. Pode ser afetado pela operação de carregamento das unidades de geração com diferentes taxas de combustível, pela combinação de operação hidráulica e térmica e pelas necessidades diárias de carga e pela venda e compra de energia. Esses custos são substancialmente controlados pelos operadores do sistema nas estratégias de despacho. Por outro lado, os custos fixos incluem investimento de capital, juros, mão de obra e outros custos independentes do sistema de carga. Os responsáveis pela operação direta do sistema têm poucos controles desses custos. Os custos de geração de energia térmica podem ser minimizados por uma estratégia de otimização conhecida como Economic Dispatch, conforme apontado por Miller (1987).
1.3. Características Ambientais
A maior parte do sistema de energia térmica opera com a minimização de custos como o alvo principal. Porém, esses sistemas queimam combustíveis fósseis, como carvão, óleo, gás ou a combustão desses combustíveis. Eles produzem emissões atmosféricas cuja natureza e qualidade dependem do tipo de combustível. Essas emissões afetam a saúde humana e também a vegetação, os animais, os recursos hídricos, etc. Também importante é o aquecimento global, segundo Talaq et al. (1994). Obviamente, é fundamental considerar as emissões na geração de energia. Analogamente ao custo de geração, a emissão pode ser minimizada por uma estratégia de otimização, conhecida como Despacho Ambiental. Freqüentemente, as emissões são proporcionais ao consumo de combustível nas unidades térmicas. A função custo também é obtida pela curva de entrada-saída da Figura 1, multiplicando a entrada de combustível pela quantidade de emissões geradas.
2. DA MODELAGEM DO PROBLEMA
2.1. Funções Objetivo
A função de custo, que é a função objetivo do problema de Despacho Econômico, é dada pela Equação (1):
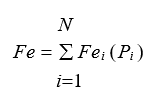
onde, 
é o custo total no conjunto de i unidades geradoras; Fei corresponde às funções de custo de cada unidade geradora i; ai, bi e ci são os coeficientes das funções de custo de cada unidade geradora i; Pi são a potência de saída de cada unidade geradora i ..
De forma análoga, a função objetivo de emissões é dada pela Equação (2):
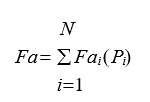
onde, Fa i ( Pi ) = d i Pi 2 + ei Pi + f i ; Fai corresponde às emissões de cada unidade geradora i; di, ei e fi são os coeficientes da função de emissões de cada unidade geradora i; Pi é a potência de saída de cada unidade geradora i.
2.2. Restrições
Um tratamento clássico para ambos, Despacho Econômico e Ambiental deve satisfazer as seguintes restrições:
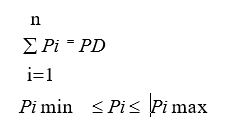
Onde PD é a demanda de energia; Pimin e Pimax são, respectivamente, o inferior e o superior das unidades de geração.
Uma vez que as funções objetivo e restrições são conhecidas para o problema de Despacho Econômico e Ambiental, há uma grande quantidade de possibilidades para resolver o problema, como o Despacho Ambiental puro, Despacho Econômico puro, Despacho Econômico com Restrições Ambientais, Despacho Ambiental com Restrições Econômicas ou ambos, simultaneamente. A última proposição descreve um problema de otimização multiobjetivo.
No presente trabalho, duas considerações são feitas para solucionar o problema. O primeiro considera o Despacho Econômico com Restrições Ambientais. Na segunda proposição, é considerado o Problema Multiobjetivo de Despacho Ambiental / Econômico.
3. PROBLEMA DE GERAÇÃO DE ENERGIA
3.1. Despacho econômico com restrições ambientais
Nesse caso, o objetivo é minimizar o custo total da geração termelétrica, considerando os limites operacionais das unidades geradoras. A demanda de energia deve ser atendida e as restrições ambientais são limitadas a um valor máximo permitido. O modelo proposto é apresentado na Equação abaixo:
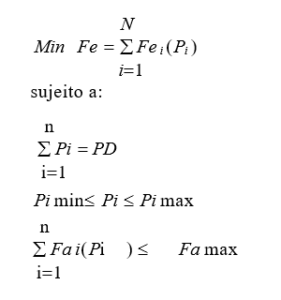
onde, Fa max corresponde ao valor máximo de emissão.
3.2. Problema de despacho ambiental / econômico multiobjetivo
Na solução de problemas de otimização simultâneos com funções de múltiplos objetivos, as dificuldades inerentes são os objetivos conflitantes, como mencionado em Van Veldhuizen et al. (2003) e Zitzler et al. (2003). No caso particular do problema de Despacho Ambiental / Econômico, minimizar o custo de geração não é a melhor estratégia do ponto de vista ambiental e vice-versa. A formulação multiobjetivo para este problema é proposta na Equação (5).
Neste problema, devido aos múltiplos objetivos, não existe uma solução ótima única, mas um conjunto de soluções conhecido como Frente de Pareto. Este conjunto é composto por soluções viáveis em que qualquer melhoria (redução) em um objetivo ocorra junto com a degradação (aumento) em, pelo menos, um dos outros objetivos. Conhecidos dois candidatos “x” e “y” de um problema com os objetivos Fi e Fj:
Nesse caso, x não é superior e também não é inferior a y. Essas soluções são chamadas de soluções não inferiores, soluções eficientes ou soluções admissíveis. O plano inferior delimitado pelas funções objetivo corresponde ao “mínimo” ou à Frente de Pareto ótima para problemas multiobjetivos.
4. Algoritmos Genéticos Auto Adaptativos
4.1. Algoritmos Genéticos
Existem muitas semelhanças entre os mecanismos de evolução e os problemas de otimização. A seleção natural é essencial para eleger os indivíduos mais bem preparados. No entanto, a natureza está em constante evolução e nenhum indivíduo pode ser visto como um indivíduo totalmente ajustado. Desta forma, o indivíduo está em constante evolução para um “novo” ótimo. Em seguida, as soluções iniciais dos Algoritmos Genéticos criados por Holand (1975), seguem para um ótimo da mesma forma que os indivíduos de uma população seguem para se adequarem ao ambiente onde vivem. Algoritmos Genéticos Adaptativos.
4.2. Metodologia Utilizada
O algoritmo genético híbrido auto-adaptativo para solução de problemas de Despacho Ambiental / Econômico possui duas rotinas operando em paralelo, a rotina Algoritmo Genético Híbrido (AGH) e a rotina Algoritmo Auto-Adaptativo (SAA). A rotina principal do AGH leva em consideração que Algoritmos Genéticos podem ser combinados com várias técnicas de busca local para formar um sistema híbrido, e para utilizar as características de busca global dos Algoritmos Genéticos e também dos mecanismos de busca local. As etapas simplificadas da rotina principal AGH são apresentadas a seguir.
4.3. Geração Inicial de População
Os indivíduos da população inicial são as forças, Pi, representados por números reais. A população inicial é encontrada usando a Equação (7):
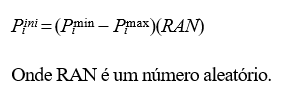
4.4. Determinação Gradiente
O gradiente é calculado usando a função de penalidade:
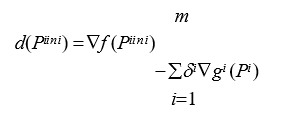
onde 
= 0 para os individuos no domínio viável. Caso contrário, apresenta um fator de penalidade.
4.5. Operador de Mutação
A mutação é o principal operador deste HGA. Este operador produz indivíduos modificados Pimod, de forma que:
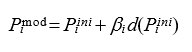
onde 
representa o tamanho do passo na direção do gradiente.
4.6. Operador de Crossover
É feita uma combinação aritmética entre os indivíduos da população inicial e os provenientes da mutação, gerando os indivíduos da nova população, conforme apresentado a seguir:
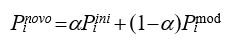
4.7. Seleção
Durante o processo de avaliação, os indivíduos são selecionados pelo Método da Roleta, para participar da população inicial da próxima geração, respeitando o número original de indivíduos da população.
4.8. Critérios de Parada
Os procedimentos são repetidos até que uma tolerância seja satisfeita ou até que um número máximo de gerações (iterações) possa ser encontrado.
4.9. Parâmetros de Controle
A rotina de controle SAA foi implementada com o objetivo de determinar iterativamente os parâmetros ótimos para a rotina HGA. Os parâmetros são determinados automaticamente, sem a necessidade de um grande número de estimativas do usuário. Tais parâmetros são NIND – número de indivíduos da população e NI – número de iterações HGA. Nesta rotina os parâmetros são gerados aleatoriamente e participam de um processo adaptativo onde evoluem ao mesmo tempo que as soluções.
4.10. Parâmetros de geração de população inicial
Duas populações de indivíduos NIND e NI são criadas aleatoriamente em um espaço relativamente grande, gerando, então: –
População dos parâmetros 1: NIND1, NI1
População dos parâmetros 2: NIND2, NI2
4.11. Parâmetros de Crossover
Indivíduos das populações de parâmetros 1 e 2, selecionados para participar do cruzamento pelo método da roleta, geram uma população de parâmetros como acima:
5. Estudo de Caso – Seis Unidades Geradoras.
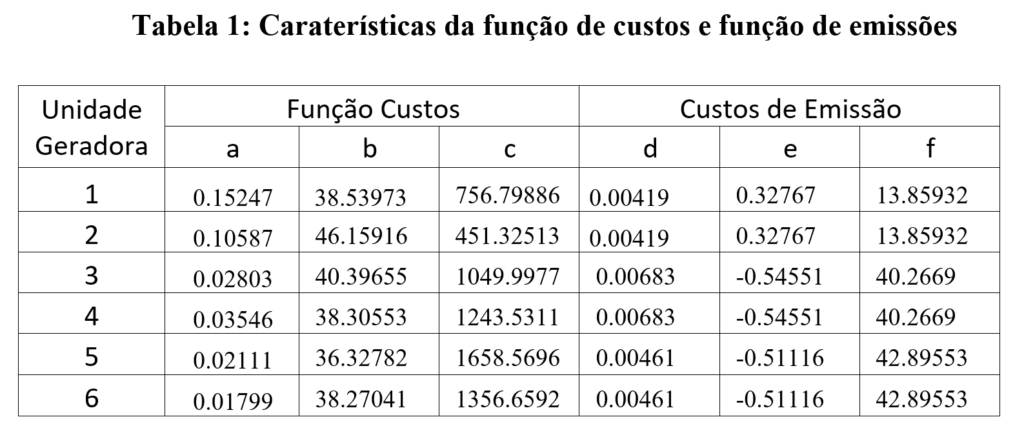
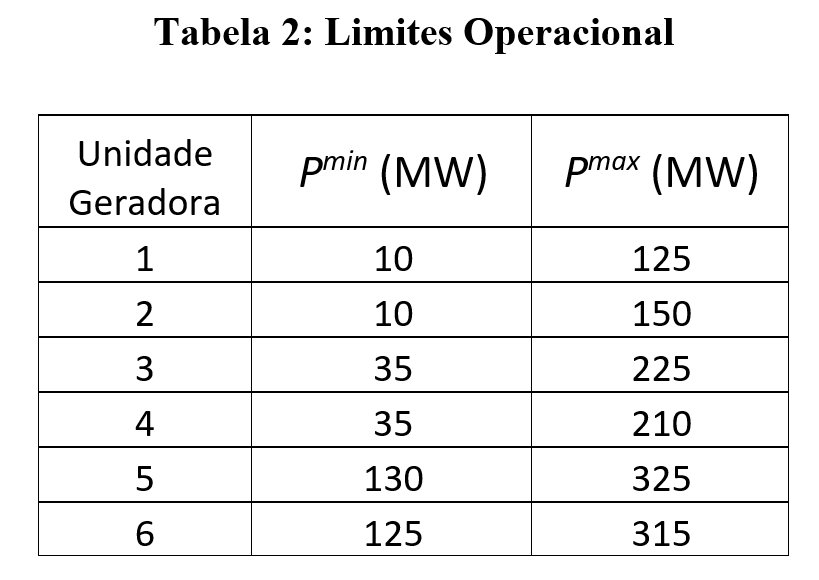
O algoritmo desenvolvido foi utilizado para encontrar o conjunto da melhor relação custo / emissão pela alocação de uma demanda de 500,0 MW entre seis unidades de geração disponíveis, respeitando seus limites operacionais. As características da função de custo e da função de emissão são apresentadas na Tabela 1. Os limites operacionais das unidades de geração são apresentados na Tabela 2. Este caso foi apresentado inicialmente por Dhillon et al. (1993). Nas próximas tabelas, P é dado em MW, o custo é dado em $/h e emissões em kg/h.
5. Resultados
5.1. Resultados do despacho econômico com restrições ambientais
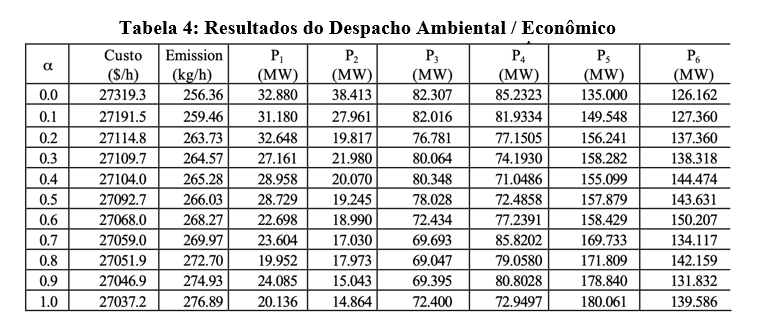
Os resultados da Tabela 3 foram obtidos por meio de alterações dos valores de Famax.
Tabela 3: Resultados do despacho econômico com restrições ambientais
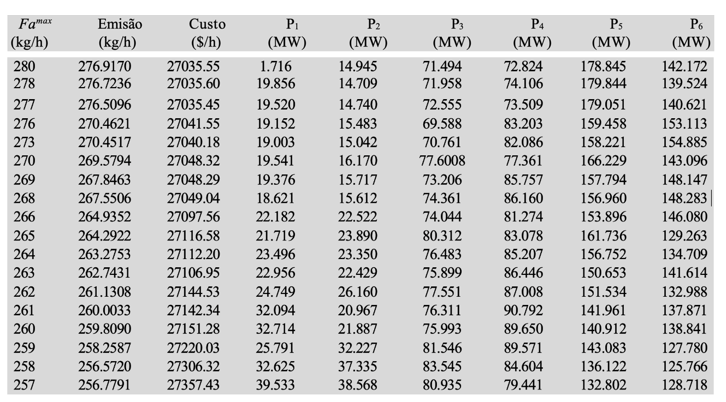
A curva de relação entre custo e emissão é mostrada na Figura 2.
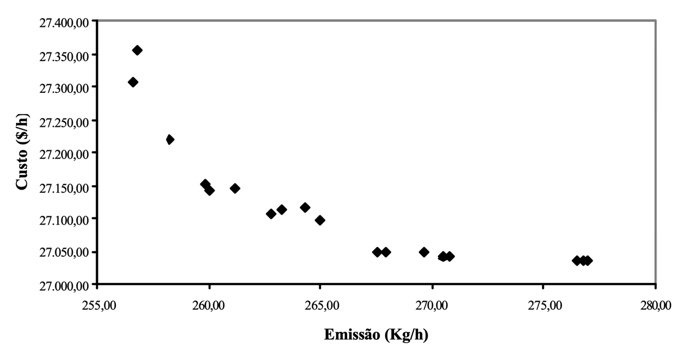
Figura 2: Resultados do despacho econômico com restrições ambientais
5.2. Resultados do despacho econômico com restrições ambientais
Os resultados da Tabela 4 foram obtidos por meio da variação do 
, de zero (0) a um (1).
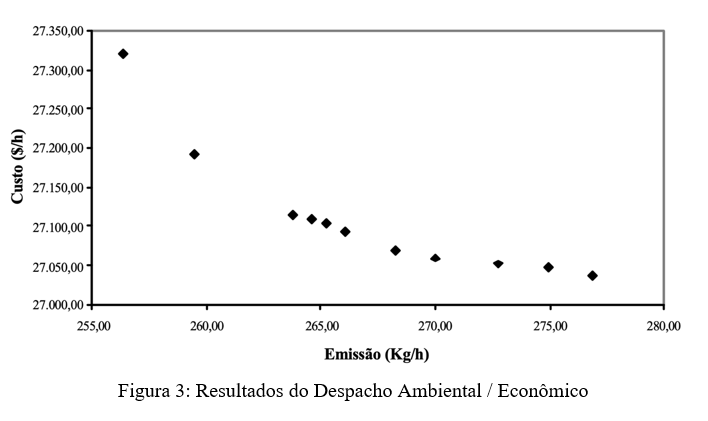
A Figura 3 mostra a relação entre custo e emissão.
6. CONCLUSÃO
Apresentamos o Algoritmo Genético Híbrido Auto Adaptativo para resolver problemas no Despacho Econômico com Restrições Ambientais e o Despacho Ambiental / Econômico. O algoritmo se ajustou muito bem a esse tipo de problema. A codificação real permitiu o uso de técnicas determinísticas, como a hibridização.
O método do gradiente formulado pela função de penalidade garantiu dois critérios importantes. Primeiramente, foi possível tratar os indivíduos inviáveis, trazendo-os ao domínio viável pela direção do gradiente negativo. Em segundo lugar, foi possível modificar os factíveis pela direção do gradiente positivo. Esse fato confirma o real significado da mutação que é introduzir uma variedade na população. O controle dos parâmetros resultou em respostas extremamente precisas, sem necessidade de estimativa dos parâmetros. Dessa forma, o algoritmo se tornou mais rápido, confiável e melhorou a usabilidade. Este algoritmo contempla um número considerável de possibilidades de operação, e ambas as abordagens comprovam a relação entre custo e emissões.
7. APLICAÇÃO
Esta solução é aplicável aos controles industriais através da Aplicação do X-Machine RTO uma plataforma que integra de forma genuína os sistemas de automação e controle da indústria de forma a transformá-los em sistemas extremamente inteligentes, reduzindo esforços de investimentos em novos sistemas ou retrofits tecnológicos.
Temos orgulho em afirmar que entregamos mais que inteligência, entregamos aumento de lucratividade!
Por: Dr. Eng. Douglas Mariani / Eng. Nicolas Goulart.
